Benford's law applied to images
(Januari 26 2021)

While watching some show called Connected on netflix. I got interested in this thing called Benford's law in the show.
Mostly my initial response was: wait this won't work, if you look up the constraints for when the law is meaningful, it shouldn't work on images at all. But I couldn't help myself to try it out myself anyway. Few hours later I had a working image processing program and called it img2benford. It reads png and jpeg files and then plots out the graph with most significand digits.
The algorithm is really simple. Open an image, iterate over each pixel. Add the red, green and blue values of that pixel giving you a 'pixel_value'. Now in this pixel_value take the most significand digit (the first one). And keep a counter for each pixel you have read with msd's: 1..9. Then at the end plot a graph with the percentage that each digit occured. Now for a random stream of numbers you get what you expect. Each msd occors about the same number of times.
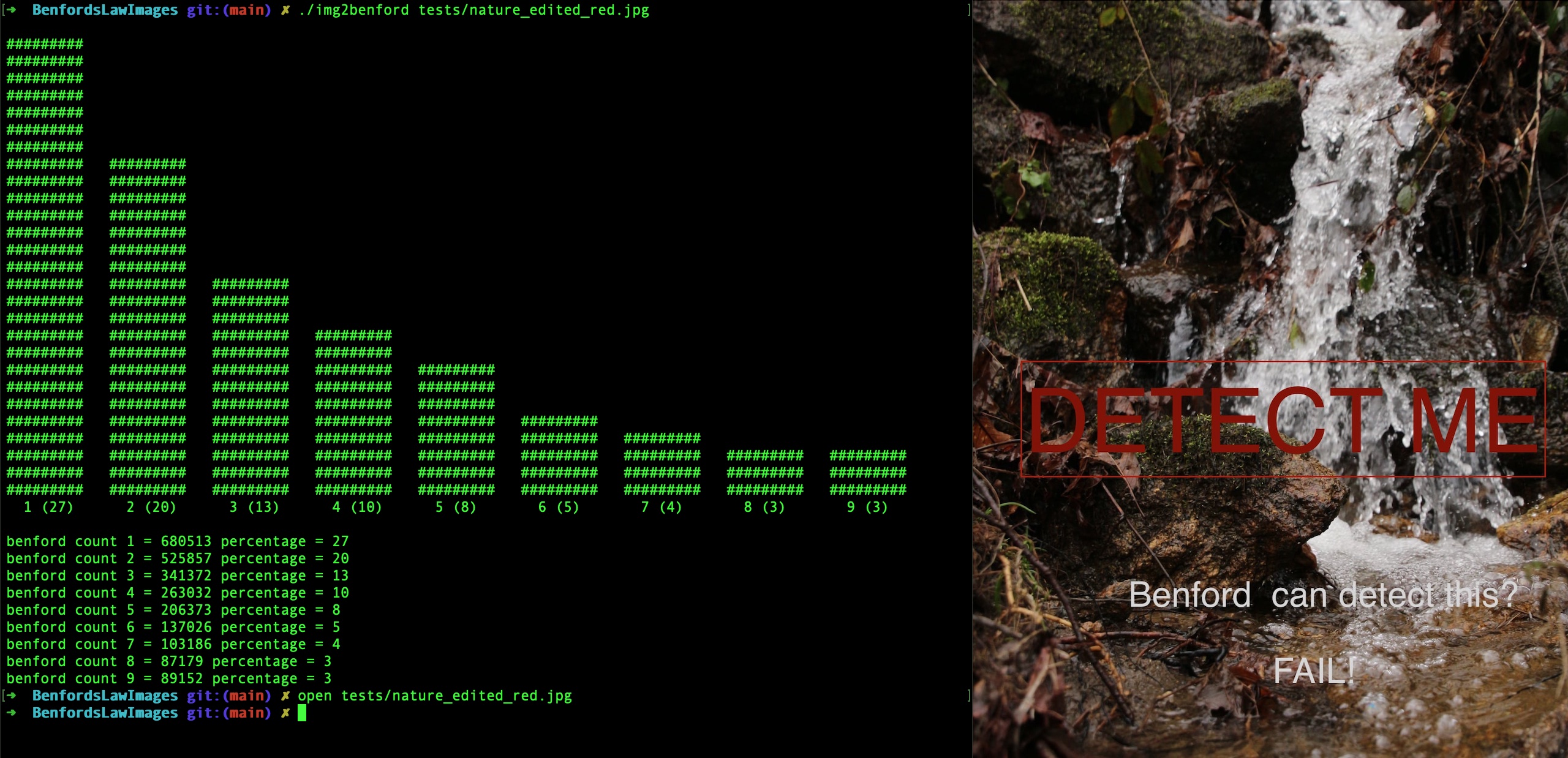
After selecting a real 'most likely not edited' nature image, I took a random picture of a waterfall in nature just from facebook. Ran the created program ./img2benford nature_photo.jpg and low and behold it did indeed plot this nice curve the whole netflix show was about.
Pretty cool right? Well turns out the show went a bit too far in providing its usecases and significance. It says whenever you edit an image and re-save it that the curve would be different. Well that didn't happen in my tests. I edited the nature picture. Put some big red text inside, resaved and reran my test on the modified image. Unfortunately it didn't improve nor worsen the curve it much. It even improved, normally digit 1 should be around 30%. However the orinal has 25% of 1's and the edited one has 27%. It should have changed the other way around instead of the current results we have.
The little program does however really work. Testing it on other images does indeed give different plots:

It also has the built in functionality to run the same test+plot on 1 million random values and this gives a plot you would normally expect to see for some random picture also:
$ ./img2benford -random
Uniform random benford plot on a million values:
######### ######### ######### ######### ######### ######### ######### #########
######### ######### ######### ######### ######### ######### ######### ######### #########
######### ######### ######### ######### ######### ######### ######### ######### #########
######### ######### ######### ######### ######### ######### ######### ######### #########
######### ######### ######### ######### ######### ######### ######### ######### #########
######### ######### ######### ######### ######### ######### ######### ######### #########
######### ######### ######### ######### ######### ######### ######### ######### #########
######### ######### ######### ######### ######### ######### ######### ######### #########
######### ######### ######### ######### ######### ######### ######### ######### #########
######### ######### ######### ######### ######### ######### ######### ######### #########
######### ######### ######### ######### ######### ######### ######### ######### #########
1 (10) 2 (11) 3 (11) 4 (11) 5 (11) 6 (11) 7 (11) 8 (11) 9 (11)
benford count 1 = 100136 percentage = 10
benford count 2 = 110687 percentage = 11
benford count 3 = 110571 percentage = 11
benford count 4 = 110709 percentage = 11
benford count 5 = 111258 percentage = 11
benford count 6 = 111325 percentage = 11
benford count 7 = 111212 percentage = 11
benford count 8 = 111025 percentage = 11
benford count 9 = 111092 percentage = 11
And yes for the observant person. Indeed 0 is not shown here, and this accounts for the missing bar on the 1. But we do see pretty much each MSD (most significant digit) get's about the same amount of counts.
Here's the output when I ran it for the first time on an image of a waterfall in a forrest (pulled from facebook, picture was taken by Jenke Goffa:
./img2benford tests/nature_image.jpg
#########
#########
#########
#########
######### #########
######### #########
######### #########
######### #########
######### #########
######### #########
######### #########
######### #########
######### ######### #########
######### ######### #########
######### ######### #########
######### ######### ######### #########
######### ######### ######### #########
######### ######### ######### ######### #########
######### ######### ######### ######### #########
######### ######### ######### ######### #########
######### ######### ######### ######### ######### #########
######### ######### ######### ######### ######### ######### #########
######### ######### ######### ######### ######### ######### ######### ######### #########
######### ######### ######### ######### ######### ######### ######### ######### #########
######### ######### ######### ######### ######### ######### ######### ######### #########
1 (25) 2 (21) 3 (13) 4 (10) 5 (8) 6 (5) 7 (4) 8 (3) 9 (3)
benford count 1 = 648313 percentage = 25
benford count 2 = 531042 percentage = 21
benford count 3 = 351602 percentage = 13
benford count 4 = 273866 percentage = 10
benford count 5 = 211944 percentage = 8
benford count 6 = 127823 percentage = 5
benford count 7 = 106355 percentage = 4
benford count 8 = 89524 percentage = 3
benford count 9 = 91162 percentage = 3
Conclusion
It's not as useful as image tampering detector as the netflix show promises, but it's indeed a pretty interesting/unexpected result. It probably might work better if you could use it on a set of similar or related images and you try finding the 'odd one out' by progressively adding some until the curve changes a lot. The github repository is here so you can geek out and try this yourself :https://github.com/w-A-L-L-e/BenfordsLawImages
Anyway if you watched the show. And also feel like seeing this law in action for yourself on some of your own images. Just checkout the above github project, build it and run it on your system. Somehow even if it doesn't work exactly like advertised, it's still a fun thing try out ;)
And ofcourse if you want to make improvements or more features or contribute, feel free to do so.